
| 
| |||
| (Fig. 1) | (Fig. 2) |
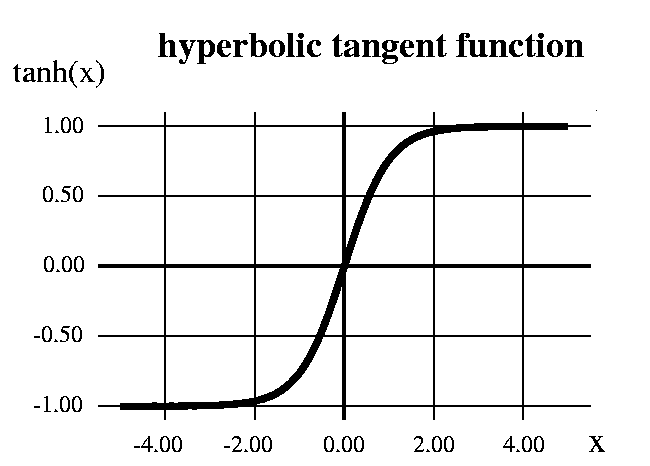
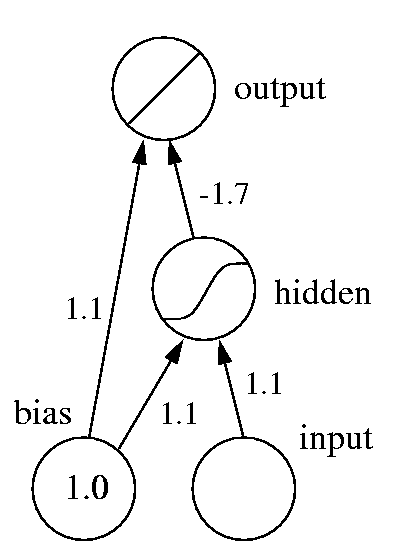
FIg. 2 shows our new network: an extra node (unit 2) with tanh activation function has been inserted between input and output. Since such a node is "hidden" inside the network, it is commonly called a hidden unit. Note that the hidden unit also has a weight from the bias unit. In general, all non-input neural network units have such a bias weight. For simplicity, the bias unit and weights are usually omitted from neural network diagrams - unless it's explicitly stated otherwise, you should always assume that they are there.
 (Fig. 3)
(Fig. 3)
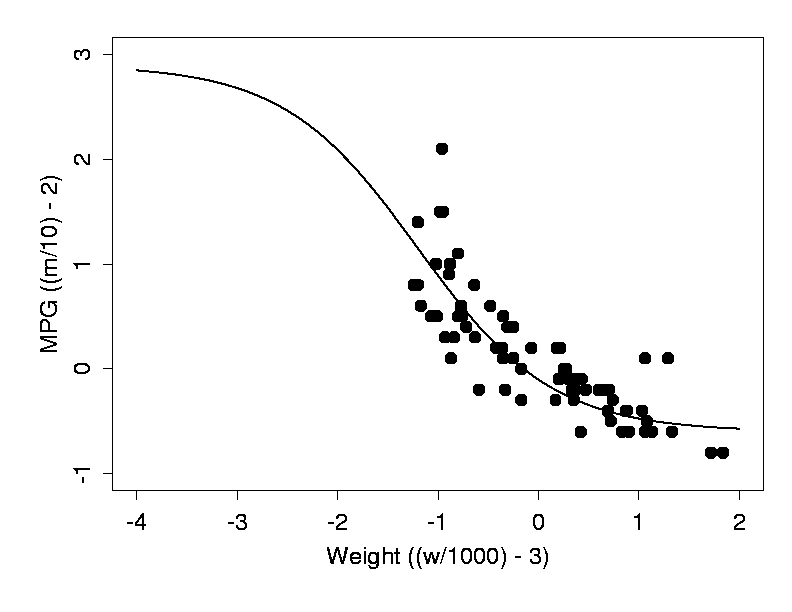
When this network is trained by gradient descent on the car data, it learns to fit the tanh function to the data (Fig. 3). Each of the four weights in the network plays a particular role in this process: the two bias weights shift the tanh function in the x- and y-direction, respectively, while the other two weights scale it along those two directions. Fig. 2 gives the weight values that produced the solution shown in Fig. 3.
 (Fig. 4)
(Fig. 4)
(Relative concentration of NO and NO2 in exhaust fumes as a function
of the richness of the ethanol/air mixture burned in a car engine.)
Obviously the tanh function can't fit this data at all. We could cook up a special activation function for each data set we encounter, but that would defeat our purpose of learning to model the data. We would like to have a general, non-linear function approximation method which would allow us to fit any given data set, no matter how it looks like.
 (Fig. 5)
(Fig. 5)
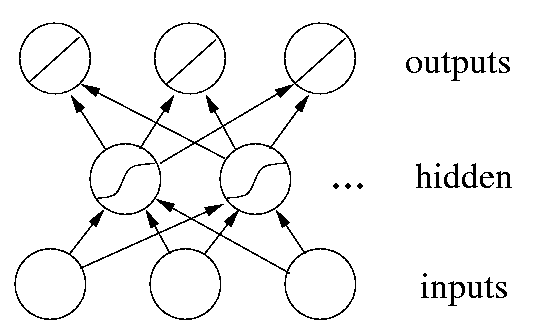
Fortunately there is a very simple solution: add more hidden units! In fact, a network with just two hidden units using the tanh function (Fig. 5) can fit the dat in Fig. 4 quite well - can you see how? The fit can be further improved by adding yet more units to the hidden layer. Note, however, that having too large a hidden layer - or too many hidden layers - can degrade the network's performance (more on this later). In general, one shouldn't use more hidden units than necessary to solve a given problem. (One way to ensure this is to start training with a very small network. If gradient descent fails to find a satisfactory solution, grow the network by adding a hidden unit, and repeat.)
Theoretical results indicate that given enough hidden units, a network like the one in Fig. 5 can approximate any reasonable function to any required degree of accuracy. In other words, any function can be expressed as a linear combination of tanh functions: tanh is a universal basis function. Many functions form a universal basis; the two classes of activation functions commonly used in neural networks are the sigmoidal (S-shaped) basis functions (to which tanh belongs), and the radial basis functions.